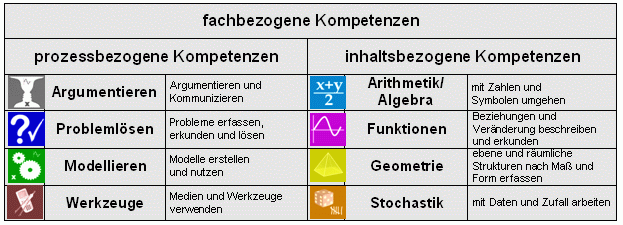
In vielen Bereichen werden mathematische Modelle benutzt: Geometrische Modelle helfen bei der Erstellung von Gebäuden, stochastischeModelle unterstützen die Meteorologen bei der Erstellung der Wettervorhersage, Populationsmodelle lassen Prognosen zu, wie sich bestimmte Populationen unter vorgegebenen Umständen entwickeln. Die Anwendungen mathematischer Modelle sind sehr weit gestreut. Auch in der Schule werden häufig Mathematische Modelle zum Thema gemacht. Während für den Anwender lediglich die Nutzung des Modells interessant ist, sollte in der Schule auch der Weg zum Modell, die Modellbildung, behandelt werden. In Nordrhein-Westfalen wurde mit der Einführung der Kernlehrpläne im Jahre 2005 dem Modellbildungsaspekt insofern eine große Bedeutung zugesprochen, als das Modellieren zu einer von fünf prozessbezogenen Kompetenzen gehört.
Allerdings findet man nur sehr selten in Schulbüchern Beiträge, in denen ein Modell komplett hergeleitet wird. Gerade hier erscheint es notwendig, entsprechendes Material zur Verfügung zu stellen, um den Prozess der Modellbildung im Unterricht behandeln zu können. Auf den folgenden Seiten werden Wege aufgezeigt, wie ausgehend von Beobachtungen in der Realität über Simulationen und deren Analyse mathematische Modelle entwickelt werden können.
Im Bereich der Biowissenschaften wird dabei zum Beispiel untersucht, wie sich Populationen entwickeln. In der Chemie werden umkehrbare Reaktionen im Gleichgewichtszustand betrachtet.

