[an error occurred while processing this directive] LEHRSTUHL A FÜR MATHEMATIK Analysis und Zahlentheorie

[an error occurred while processing this directive]

---

  English version

---

Schülertage im Sommersemester 03

• Startseite
• Erster Tag - komplexe Zahlen
• Zweiter Tag - Fibonaccizahlen
• Dritter Tag - pythagoräische Tripel

Dritter Tag: Pythagoräische Tripel

Vorlesung und Aufgabenblatt

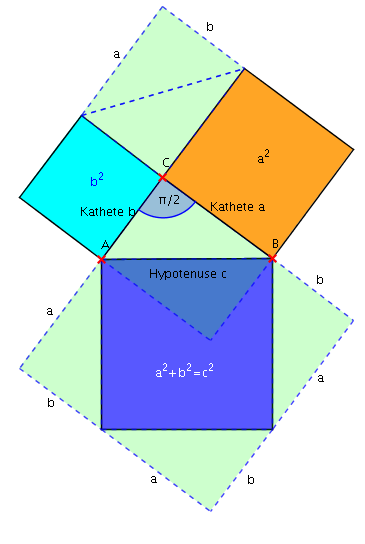
Zur Vorlesung zum Thema pythagoräische Tripel gibt es ein kurzes Skript.

Das Aufgabenblatt gibt es hier als ps-Datei und als pdf-Datei.

Aufgaben:

• Führen Sie den Beweis des hier verlinkten Satzes(Hyppocrates' Lunar) aus. Verwenden Sie dazu ruhig die Behauptung aus Aufgabe 4 b).
• Betrachten Sie nebenstehende Zeichnung - können Sie erkennen, was sie mit einem Beweis des Satzes von Pythagoras zu tun hat?
• Es gibt viele geometrische "Beweise" des Satzes von Pythagoras, nennen Sie 5 davon! Und damit das nicht so schwer wird, schauen Sie ruhig unter dieser Beweisseite nach.
• Wieviele ganzzahlige Lösungen hat die Gleichung xⁿ+yⁿ=zⁿ abhängig von n? Der angegebene Link bietet Ihnen eine Quelle für Informationen zum Thema. Vorsicht: Das Thema ist extrem kompliziert, wenn man es ohne Hilfe vollständig lösen will.
• Nach einem Satz der heutigen Vorlesung (m und n waren eventuell in der Bedeutung vertauscht) gibt es für jedes primitive Pythagoräische Tripel Zahlen m und n, so dass x=n²-m² und y=2mn ist. Berechnen Sie m und n für das primitive pythagoräische Tripel (11999,11760,16801). Da das nun doch etwas viel im Kopf ist, probieren sie es doch mal mit diesem Rechner.
• Sollte es Ihnen etwas langweilig sein? Haben Sie die Aufgaben schon alle bearbeitet? Weiter unten haben wir noch ein paar Links für Sie angegeben, wenn da auch nichts interessantes für Sie dabei ist, können Sie ja noch einmal zu den vergangenen Tagen zurück blättern.

Ein kleiner Film zur Konstruktion pythagoräischer Dreiecke

zum Film.

Links auf diverse Seiten zu pythagoräischen Tripeln

Ein Applet, das pythagoräische Tripel berechnet, findet sich auf dieser Seite. Daneben steht eine wirklich knappe Einführung in pythagoräische Tripel, die Sie nun nicht mehr brauchen sollten.

Viele Applets zum Satz von Pythagoras und anderen geometrischen Gegebenheiten. Diese Seite enthält einige Beweise zum Satz von Pythagoras. Können Sie sie nachvollziehen?

Einführung: Ausgehend vom 3-4-5 Dreieck werden pythagoräische Dreiecke behandelt. Insbesondere wird der Inkreisdurchmesser rechtwinkliger Dreiecke mit ganzzahligen Seitenlängen und eine Erzeugungemethode für pythagoräische Tripel vorgestellt.

Ein wenig zur Geschichte

Ein paar Aufgaben rund um pythagoräische Tripel bietet diese Seite dem Besucher. Außerdem gibt es hier zwei graphische "Beweise" des Satzes von Pythagoras.

Eine Seite für Lehrer

Ein paar pythagoräische Tripel

Englischsprachige Links

Wolfram: Pythagoräische Tripel

Etwas Geschichte - Pythagoras und Irrationale Zahlen

Die Gleichung xⁿ+yⁿ=zⁿ hat abhängig von n verschieden viele ganzzahlige Lösungen (x,y,z). Hier wird ein kurzer Überblick gegeben.

Das Bild von Pythagoras wurden von der Seite http://www.matheprisma.uni-wuppertal.de/Module/Quadrat/pythagor.htm übernommen.

   Zurück zur Startseite

Haftungsausschluss Letzte Änderung: 10.07.2006, Webmaster